Lo prometido es deuda y tal y como os contaba en el post de Ideas de Actividades con las regletas numéricas de 3 a 6 años, hoy en este post os enseño más ideas esta vez encaradas para niños de 6 a 12 años.
Si es la primera vez que oyes hablar de este material te recomiendo que leas este post en el que podrás ver de qué hablo. Además, en este otro post podrás encontrar un imprimible gratuito para hacer tus propias regletas Montessori o Cuisenaire.
1. Doble, triple y mitad con las regletas
El concepto de doble, triple y mitad es un proceso natural al acercamiento de la multiplicación y división.
Para representar el doble con las regletas solo tendremos que poner una determinada cantidad, dos veces. (o tres si estamos hablando del triple)
Para averiguar cuanto es el resultado, ponemos las dos cantidades una al lado de la otra y sustituimos la distancia por el menor número de regletas.
Para calcular la mitad haremos el proceso contrario. Colocaremos una cantidad determinada e intentaremos formarlo con dos cantidades iguales de forma exacta.

2. Multiplicar con las regletas numéricas
Para multiplicar con las regletas numéricas lo haremos creando un rectángulo cuyos lados representan los factores de la multiplicación. Para hacerlo podemos crear un marco con las regletas de los dos factores y el resultado será el rectángulo creado en el interior de este marco. Por ejemplo, si queremos multiplicar 5×6 colocaremos una regleta de 5 y una de 6 creando un marco.

De esta forma vemos de forma muy visual que el largo de la regleta que cogemos es de 5 y el número de regletas que vamos a coger es 6, por lo que cogeremos regletas todo lo que ocupa la regleta de 6, que serán 6 veces.

De esta forma, cuando los factores son iguales, vemos que se forma un cuadrado, y es algo que se cumplirá siempre, todos los números multiplicados por ellos mismos nos darán resultado un cuadrado perfecto. Con esto, estaremos teniendo nuestro primer contacto con las potencias.

Cuando el niño ya tiene claro como multiplicar con las regletas no será necesario poner cada vez el marco si no que lo harán directamente y pueden ir representando toda la tabla de multiplicar aunque para ello necesitaremos regletas de las que hay en una caja.
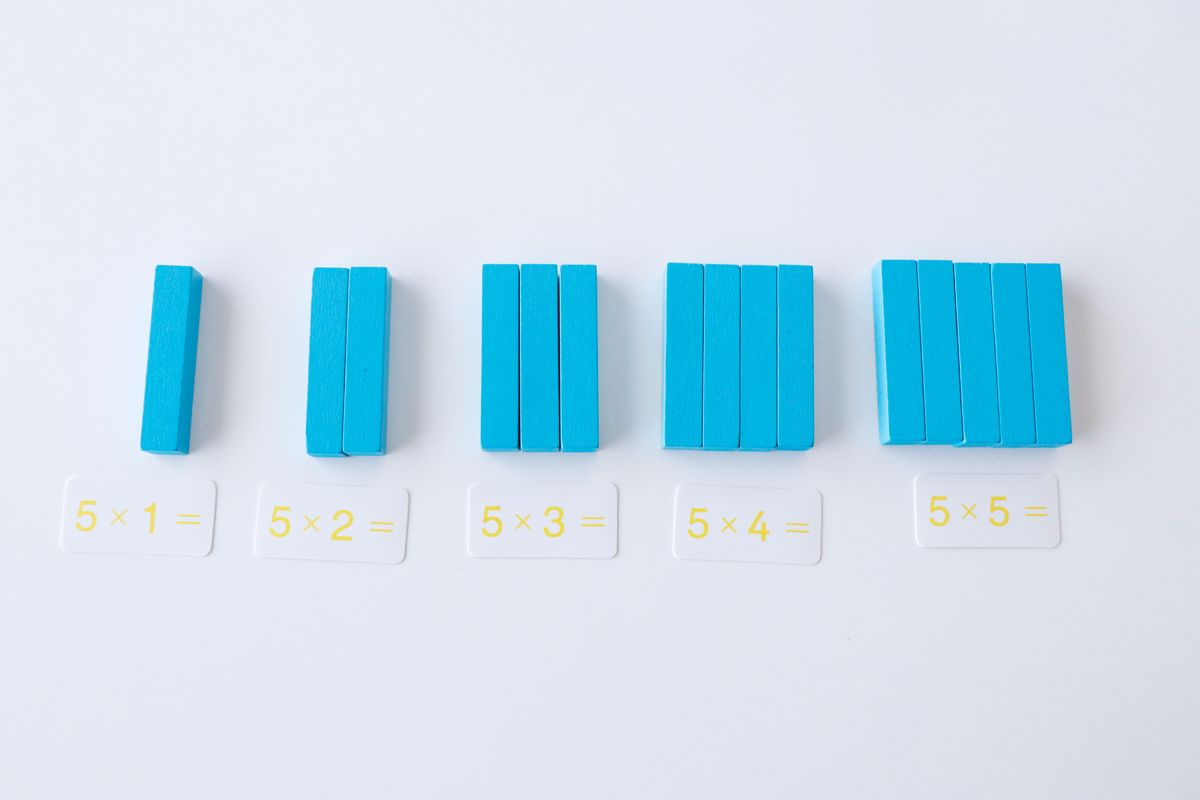
Con las regletas será muy fácil ver la multiplicación como una suma repetida de números. Para ello, en lugar de poner las regletas a modo de rectángulo como en la multiplicación lo haremos colocando las regletas una al lado de la otra como hicimos en la suma (puedes verlo en este post) y colocando debajo el resultado ultizando las menos regletas posibles.
3. Propiedad conmutativa de la multiplicación
De esta forma podremos ver muy fácilmente que el orden de los factores no altera el producto. Para comprobarlo realizaremos la multiplicación en un orden determinado y luego en el otro.
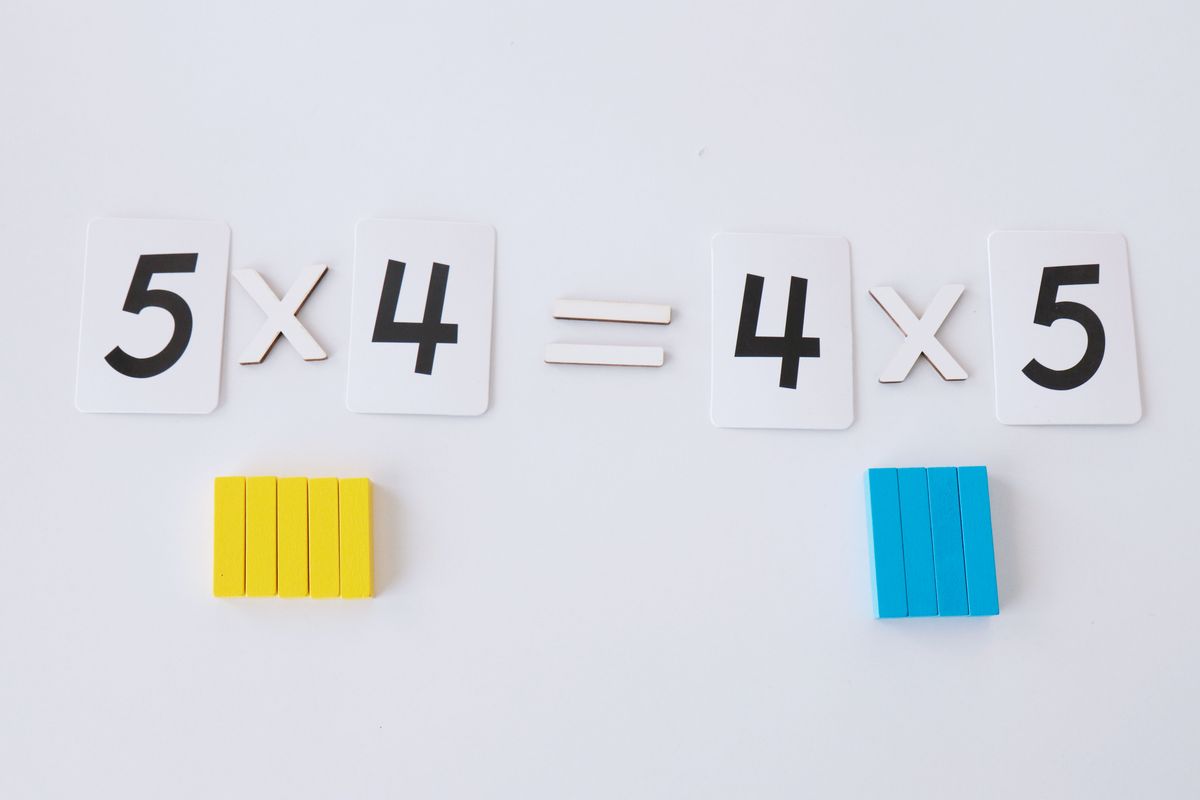
Y para comprobar que el resultado es el mismo lo ponemos uno encima del otro y vemos que ocupa exactamente el mismo espacio.

También podemos hacerlo con la técnica del marco de la siguiente forma:

4. Propiedad Asociativa de la multiplicación
Cuando tenemos una multiplicación de más de 2 factores la forma en la que agrupamos los factores no influye en el resultado. Con las regletas lo podremos demostrar de la siguiente forma.
Colocando como ejemplo la multiplicación de 4x5x3 vamos a resolverla de diferentes formas. Primero agruparemos los factores 4×5) y el multiplicaremos por 3 el resultado. Resolvemos con las regletas 4×5 cogiendo 4 veces la regleta de 5. Luego para multiplicar esto por 3 lo cogemos dos veces más para tenerlo tres veces.

Ahora vamos a asociar los factores de una forma diferente para comprobar que el resultado será el mismos. Esta vez agruparemos 5×3 así que cogeremos 5 regletas de 3. Una vez hecho lo cogeremos 4 veces ya que este resultado se multiplica por 4.

En los dos casos el resultado serán 60, formamos los prismas rectangulares cuyos lados y arista son 4, 5 y 3.

Vistos como en la foto, los prismas se ven diferentes porque uno está acostado pero si los ponemos en la misma posición se verán iguales. También podemos extenderlos para comprobar que su área (o el lugar que ocupan) es el mismo.

5. Los cuadrados de los números
Como ya habíamos visto antes, cuando multiplicamos un número por sí mismo se forma un cuadrado con las regletas. Esto lo representamos a modo de potencia con un pequeño 2 que se llama exponente. Podemos representar todos los cuadrados con las regletas:

6. La tabla Pitagórica o Decanomio Montessori
La tabla Pitagórica o decanomio Montessori es la representación de las 10 primeras tablas de multiplicar. Al representar la tabla Pitagórica con las regletas los peques podrán establecer relaciones numéricas muy interesantes. El decanomio Montessori consiste en representar tanto con las regletas como con las perlas las tablas de multiplicar en un gráfico de doble entrada, donde ponemos las tablas ordenadas en los dos ejes.

En esta representación visual del Decanomio podemos ver curiosidades como que la diagonal de esta representación contiene los cuadrados de los números. También podrán observar que esta diagonal divide la tabla en dos mitades iguales.

Comentar que con las regletas numéricas que vienen en la caja de regletas Montessori o en las Cuisenaire, no tendremos suficientes regletas para respresentar las 10 primeras tablas. Si nuestra finalidad es hacer esta actividad completa el único material que conozco que tienes las suficientes regletas para hacerlo es la caja del Decanomio con las perlas Montessori

También tenemos la representación del Decanomio de forma sensorial con la caja de la tabla de Pitágoras
7. Los cubos de los números
Otra curiosidad del Decanomio representado con las regletas es que si juntamos los brazos de cada número en la diagonal se forman los cubos de los números.


Estos cubos podremos intercambiarlos y comprobar que son los mismos con los cubos del material cúbico.

8. Dividir con las regletas numéricas
Con las regletas númericas y la ayuda de unos peones o muñequitos podemos hacer divisiones. Nosotros usamos los muñecos de Grimm’s pero puedes cualquier tipo de muñeco pequeño o los peones de algún juego de mesa. En el ejemplo queremos dividir 20 entre 5:

Para hacer la división tendremos que repartir la cantidad entre el número de peones que tenemos. Para poder hacerlo tendremos que cambiar el total de nuestra cantidad por un número de regletas igual a los peones que tenemos.

El resultado de nuestra división será lo que se lleva uno de ellos, es decir una regleta de 4.

Si la división no es exacta hacemos la repartición y dejamos lo que sobra como resto pero siempre tendremos que tener en cuenta que este resto no puede ser nunca más grande que el resultado, si nos pasa esto es que no hemos hecho la repartición bien.
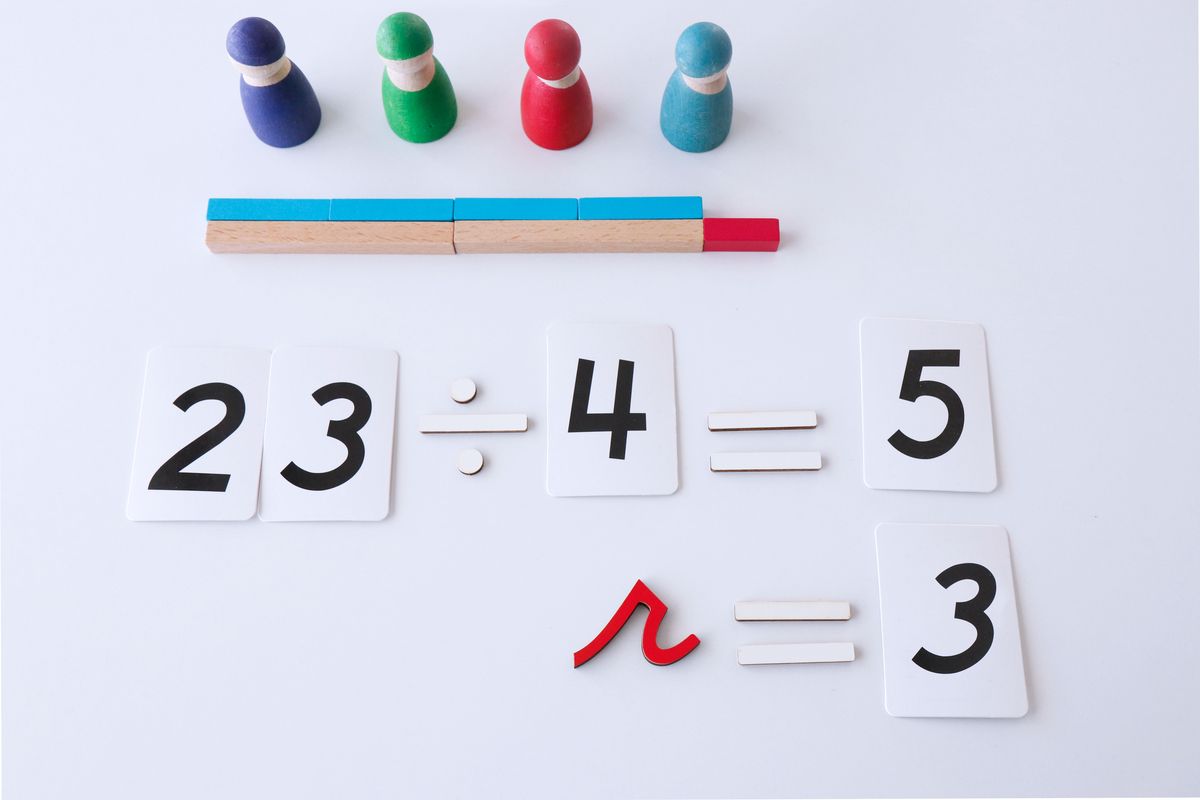
9. Multiplicación y División como operaciones inversas
Con las regletas podemos presentar de forma visual la multiplicación y división como operaciones inversas.
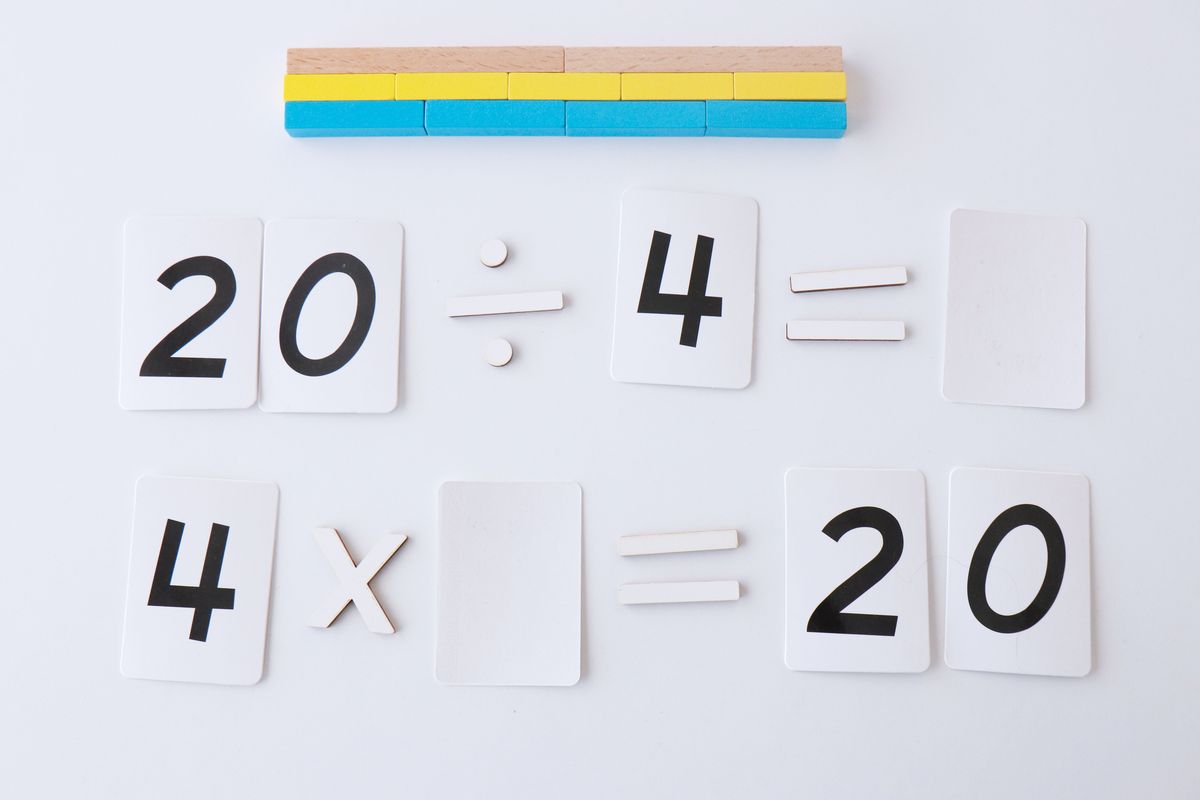
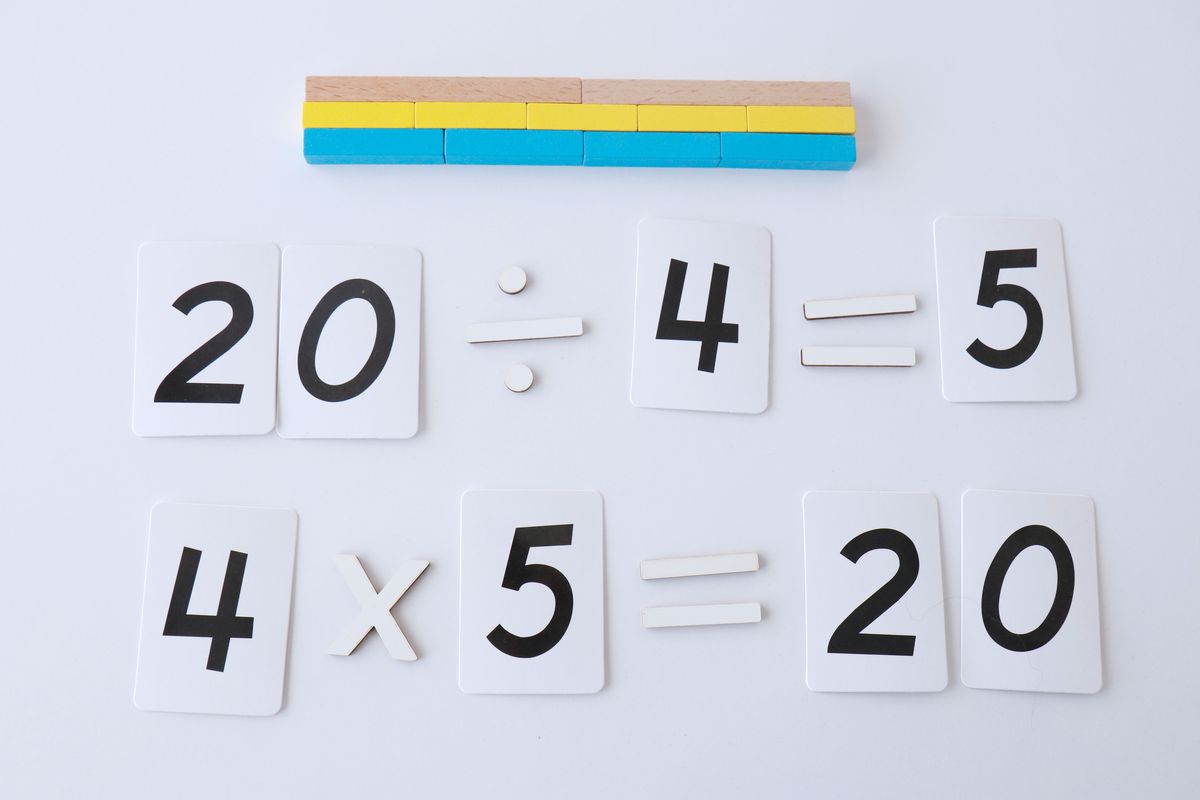
10. La media aritmética con regletas numéricas
Realizar la media aritmética con las regletas a partir de la investigación es un proceso muy completo y visual.
La media aritmética es el valor resultante de sumar ciertas cantidades y dividir el resultando por el número de cantidades que teníamos. Con las regletas podremos representar esto de la siguiente forma. En base al ejemplo tendremos los siguientes números: 3, 6, 9 y 10. Cogemos las regletas de cada uno de ellos y las sumamos. Al hacer la suma la representamos con el menor número de regletas posible, como en este caso es 28 ponemos dos regletas de 10 y uno de 8. Después intentaremos conseguir un número de regletas iguales que nos puedan permitir completar el espacio de 28.
Después de varios intentos veremos que podemos hacer el número 28 con regletas de 7 y que para ello necesitaremos 4 regletas.

Por tanto, la media aritmética de 3, 6, 9 y 10 es 7.

Una vez hecho esto por medio de la experimentación el peque podrá pensar en qué operaciones ha hecho para llegar al resultado, e incluso (dependiendo de la edad) será capaz de generar la fórmula por sí mismo. De esta manera, será un proceso mucho más rico en todos los sentidos.

11. La raíz cuadrada con regletas
La raíz cuadrada de un número es averiguar el número que multiplicado una vez por sí mismo nos da el primer número. Hacer esta operación que parece tan compleja en regletas será muy fácil y visual. Para resolver la raíz cuadrada de un número con regletas consistirá en coger este número con regletas de uno y formaremos con ellas un cuadrado exacto. Para ello empezaremos formando un cuadrado de 4 cuadrados e iremos aumentando por cada lado. Lo explico con un ejemplo.
Para hacer la raíz cuadrada de 20 cogeremos 20 regletas de 1.

Empezamos formando un cuadrado con 4 cuadraditos y vamos a ir aumentando los brazos del cuadrado de uno en uno.

Continuaremos así hasta formar el cuadrado más grande que podamos con ellos. Como podemos apreciar en la foto, el cuadrado más grande que hemos podido hacer es el cuadrado de 4, porque con los 4 cuadraditos que nos quedan no tenemos suficiente para hacer un cuadrado más grande. El resultado de la raíz nos lo da el número de cuadraditos que tiene un lado. Por tanto, la raíz cuadrada de 20 será 4 y tendremos un resto de 4.

Es un proceso que resulta muy visual y manipulativo para algo que normalmente cuesta mucho de entender para algunos peques.
12. El perímetro de una figura con regletas numéricas
Para averiguar el perímetro de una figura geométrica con regletas solo tendremos que formar este perímetro con ellas y sumarlas todas juntas.

Y eso es todo por hoy, recuerda que puedes encontrar más Actividades en el post de Ideas de actividades con las regletas Montessori para niños de 3 a 6 años.
Y en este post podrás descargar tus propias regletas numéricas para imprimir en diferentes formatos (Montessori, Cuisenaire, con divisiones y sin divisiones)
Aquí te dejo algunos enlaces que pueden ser de utilidad.
Si no queréis perderos ninguna entrada o vídeo os invito a que os suscribáis o a que nos sigáis en Facebook, Instagram o nuestro Canal de YouTube! Si te ha gustado esta entrada y crees que pudiera servirle a alguien más… COMPARTE! Gracias!!



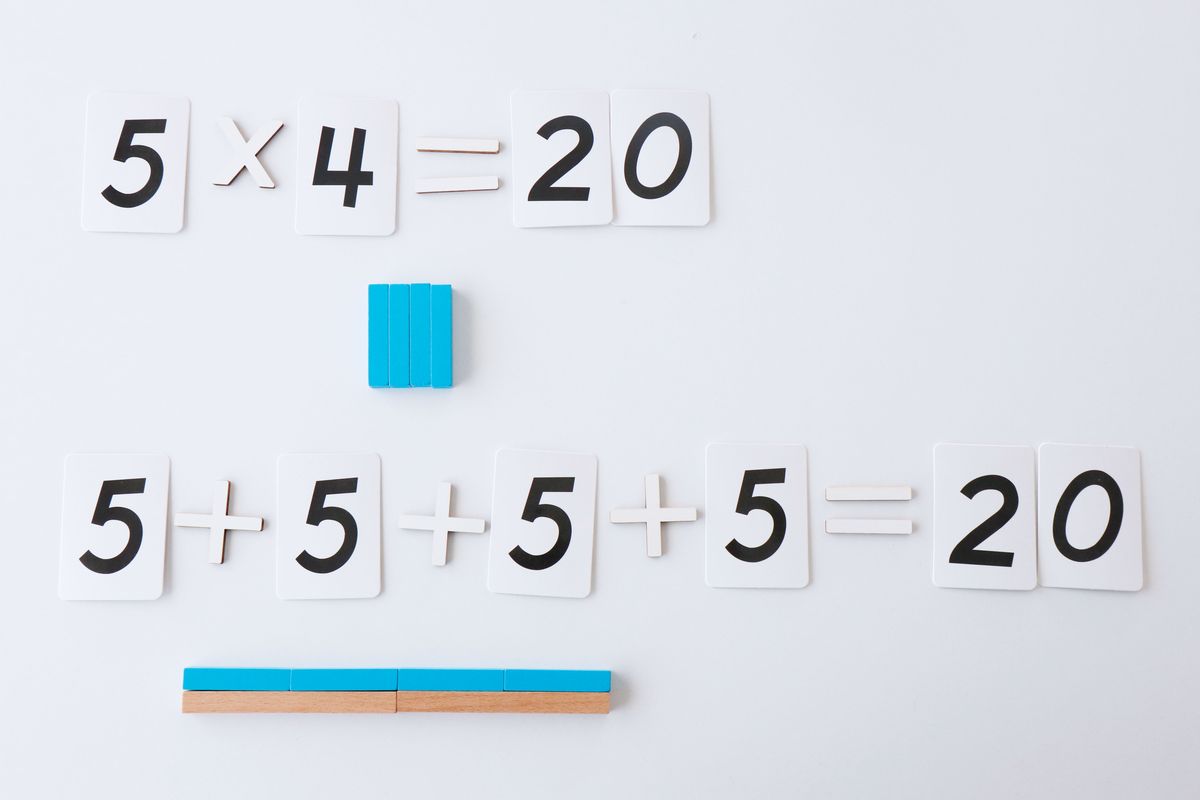






















3 comentarios. Dejar nuevo
Hola. Tengo una duda.
En la propiedad asociativa, no se están poniendo las regletas al revés? Por ejemplo, en 4*5 en lugar de coger 5 regletas de 4 (como se estaba haciendo con las multiplicaciones) cogen 4 de 5. Es lo mismo, pero a mi me genera confusión a la hora de explicar el mecanismo.
Encuentro el mismo problema en alguno de los ejemplos de la entrada de los policubos.
Muchas gracias por tus post.
Hola Nuria,
No se si te refieres en las fotos donde se representa la tabla del 5 y las etiquetas de abajo ponen 5×1, 5×2… Cuando representamos una tabla con regletas lo hacemos cogiendo solo regletas de esta tabla, y las etiquetas, realmente, deberían decir 1×5, 2×5, 3×5… Lo que pasa es que cuando hacemos la tabla con los niños no lo solemos hacer así, si no que empezamos siempre a decir el número de la tabla que estamos representando. Creo que de esta forma es más fácil luego poder hacer la comprobación que la multiplicación es una suma repetida del mismo número.
De todas formas, te diría que esto no es algo que tenga una única forma de hacerse ni de verse y que cada uno debe hacerlo como más claro e intuitivo le sea. 😉
Excelente información, porque es una ayuda muy importante para mi labor pedagógica. Gracias